Special Factoring Patterns
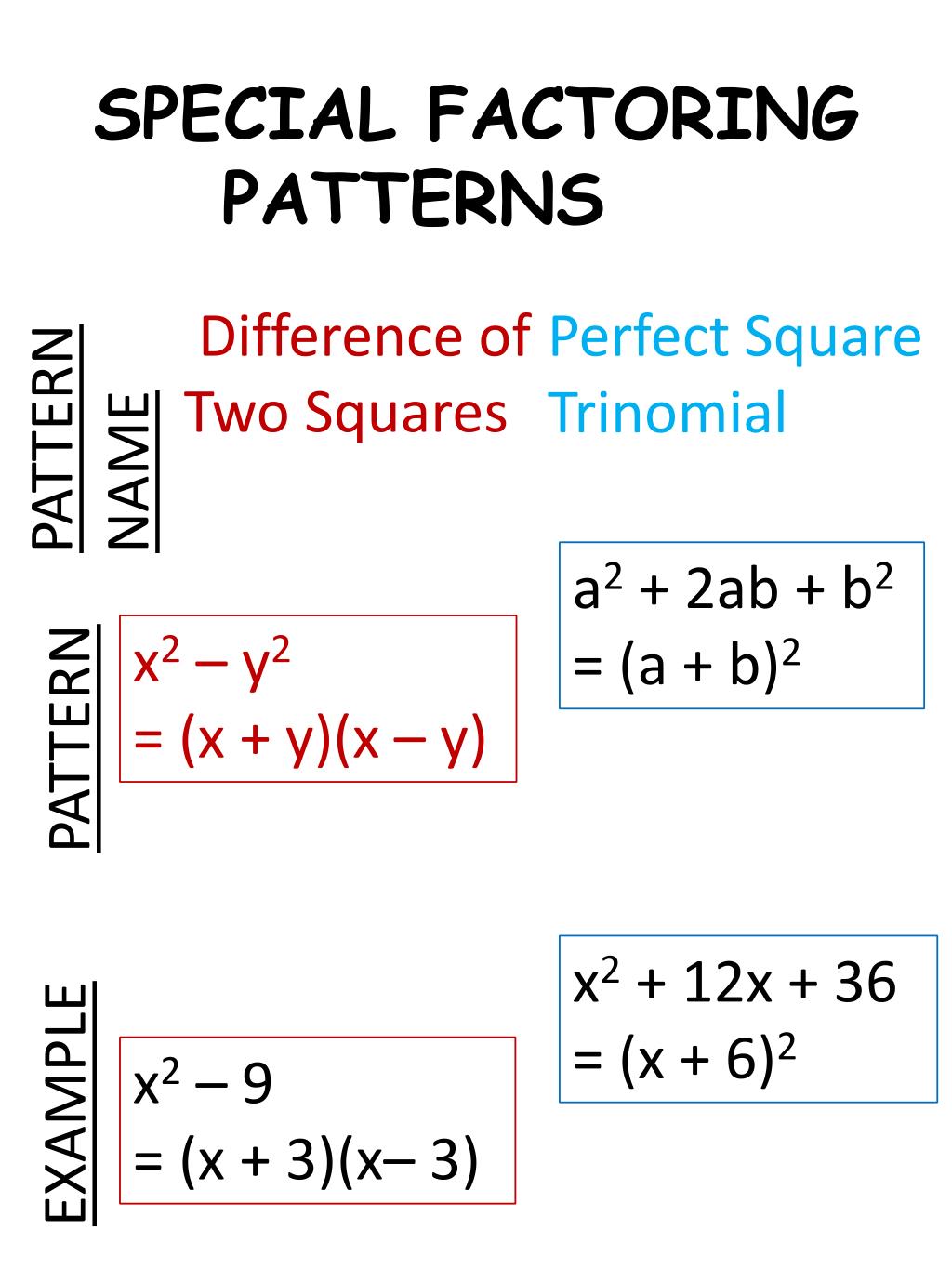
Special Factoring Patterns - Factoring by difference of squares. A3 + b3 = ( a + b ) ( a2 − ab + b2) factoring a difference of cubes: When the middle term is negative, we use the pattern a2 − 2ab +b2, a 2 − 2 a b + b 2, which factors to (a − b)2. Here are the two formulas: Sometimes, you hardly have to do any work at all to factor a polynomial. Web why learn how to factor special cases? Factoring by sum and difference of cubes. The difference of squares magic, math trick, or math principle, actually works even better than just when the numbers are only one away from the known square. Web factoring using structure involves recognizing patterns in expressions, like the difference of squares or perfect square trinomials, and using these patterns to break down complex expressions into simpler ones. A3 − b3 = ( a − b ) ( a2 + ab + b2) They're the formulas for factoring the sums and the differences of cubes. Differences of squares | purplemath. The first is the difference of squares formula. When the middle term is negative, we use the pattern a2 − 2ab +b2, a 2 − 2 a b + b 2, which factors to (a − b)2. Some people like to find patterns. Web factoring using structure involves recognizing patterns in expressions, like the difference of squares or perfect square trinomials, and using these patterns to break down complex expressions into simpler ones. Web factoring using the perfect square pattern (video) | khan academy. · factor binomials in the form of the difference of squares. Factoring by sum and difference of cubes. They're. There are some polynomials that, when factored, follow a specific pattern. Here are the two formulas: Web factoring special cases date_____ period____ factor each completely. We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. 153 views 1 year ago algebra 1 unit 10 polynomials and factoring. Some people like to find patterns in the world around them, like a game. The sign of the middle term determines which pattern we will use. If you learn to recognize these kinds of polynomials, you can use the special products patterns to. These types of binomial multiplication problems come up time and time again, so it's good to be. Web factoring with special forms is a process of using identities to help with different factoring problems. [latex] {a}^ {2}+2ab+ {b}^ {2} [/latex] a difference of squares: Differences of squares | purplemath. Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. Perfect square trinomials of the form: Web factoring using the perfect square pattern (video) | khan academy. Factor x2 out of the first two terms, and − 25 out of the second two terms. Some people like to find patterns in the world around them, like a game. Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. There. The difference of squares magic, math trick, or math principle, actually works even better than just when the numbers are only one away from the known square. If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly. We have seen that some binomials and trinomials result from special. Created by sal khan and monterey institute for technology and education. If you learn to recognize these kinds of polynomials, you can use the special products patterns to. Factor x2 out of the first two terms, and − 25 out of the second two terms. In this video, we cover the three basic special factoring patterns necessary at an algebra. 9y2 + 24y + 16. The difference of squares magic, math trick, or math principle, actually works even better than just when the numbers are only one away from the known square. A3 − b3 = ( a − b ) ( a2 + ab + b2) Factoring with the bomb method. To expand any binomial, we can apply one. [latex] {a}^ {2}+2ab+ {b}^ {2} [/latex] a difference of squares: If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly. A3 − b3 = ( a − b ) ( a2 + ab + b2) Web factoring using the perfect square pattern (video) | khan academy. Created by. The steps are summarized here. Web we have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. Factor x2 out of the first two terms, and − 25 out of the second two terms. Factoring trinomials using their coefficients. Both are divisible by 2 and by x^3. A3 − b3 = ( a − b ) ( a2 + ab + b2) Factoring using the perfect square pattern. They're the formulas for factoring the sums and the differences of cubes. 1) 16 n2 − 9 (4n + 3)(4n − 3) 2) 4m2 − 25 (2m + 5)(2m − 5) 3) 16 b2 − 40 b + 25 (4b − 5)2 4) 4x2 − 4x + 1 (2x − 1)2 5) 9x2 − 1 (3x + 1)(3x − 1) 6) n2 − 25 (n + 5)(n − 5) 7) n4 − 100 (n2 + 10)(n2 − 10) 8) a4 − 9 (a2 + 3)(a2 − 3) 9) k4 − 36 (k2. Web why learn how to factor special cases? These types of binomial multiplication problems come up time and time again, so it's good to be familiar with some basic patterns. There are some polynomials that, when factored, follow a specific pattern. · factor trinomials that are perfect squares. One of the keys to factoring is finding patterns between the trinomial and the factors of the trinomial. ( a + b) 2 = a 2 + 2 a b + b 2. Differences of squares | purplemath.
Factoring Special Patterns YouTube

Algebra 2 Unit 3 Day 5 Factoring Special Patterns and Grouping

Lesson 3 Special Factoring Patterns YouTube
Factoring INB Pages Mrs. E Teaches Math

IM3Special Factoring Patterns YouTube

Ch.11.6 Special Factoring Patterns
PPT Chapter 6 Section 4 Factoring and Solving Polynomials Equations

Factoring Formulas in Algebra What Are Factoring Formulas?

Special factoring patterns YouTube

Special factoring patterns YouTube
The Difference Of Squares Magic, Math Trick, Or Math Principle, Actually Works Even Better Than Just When The Numbers Are Only One Away From The Known Square.
Perfect Square Trinomials Of The Form:
Some People Like To Find Patterns In The World Around Them, Like A Game.
Web Factoring Special Cases Date_____ Period____ Factor Each Completely.
Related Post: