What Is The Sum Product Pattern
What Is The Sum Product Pattern - Web what is the sum product pattern? This document explain the method, called either the ac method or the product. Web this is the pattern for the sum and difference of cubes. Sums and products of roots. Web the product sum method of factoring we use on trinomials (ax 2 +bx+c) with the value of a=1. We just developed special product patterns for binomial squares and for the product of conjugates. This is the method that is probably used the most. ( a + b ) ( a + b) = a ² + 2 ab + b ². There are a finite number. We will write these formulas first and then check them by multiplication. Web factoring out common factors. We will write these formulas first and then check them by multiplication. This document explain the method, called either the ac method or the product. Web the product sum method of factoring we use on trinomials (ax 2 +bx+c) with the value of a=1. We just developed special product patterns for binomial squares and for. A2 + 2ab +b2 = (a + b)2 a2 − 2ab +b2 = (a − b)2 a. This document explain the method, called either the ac method or the product. Web recognize and use the appropriate special product pattern. If the polynomial is of the form x 2 + b x +. Web factoring out common factors. 68 = 22 ∗ 17 68 = 2 2 ∗ 17 so the only options are 1 1 and 22 ∗ 17 = 68 2 2 ∗ 17 = 68, or 2 2 and 2. Web here is the pattern—the reverse of the binomial squares pattern. Web cos(α − β) = cosαcosβ + sinαsinβ − cos(α + β) _ =. Therefore, ( a + b )² = a ² + 2 ab + b ². = 6 x 2 + 3 x = 3 x ( 2 x + 1) . We will write these formulas first and then check them by multiplication. Web cos(α − β) = cosαcosβ + sinαsinβ − cos(α + β) _ = − (cosαcosβ −. Web the product sum method of factoring we use on trinomials (ax 2 +bx+c) with the value of a=1. Web what is the sum product pattern? Web factoring out common factors. There are a finite number. A root (or zero) is where the polynomial is equal to zero: If each term in the polynomial shares a common factor. If the polynomial is of the form x 2 + b x + c. Sums and products of roots. = 6 x 2 + 3 x = 3 x ( 2 x + 1) . Because there are factor nodes and variables nodes, we have two types of messages: Web what is the sum product pattern? ( a + b ) ( a + b) = a ² + 2 ab + b ². Web the product sum method of factoring we use on trinomials (ax 2 +bx+c) with the value of a=1. If the polynomial is of the form x 2 + b x +. Because there are. There are a finite number. Therefore, ( a + b )² = a ² + 2 ab + b ². Web cos(α − β) = cosαcosβ + sinαsinβ − cos(α + β) _ = − (cosαcosβ − sinαsinβ) cos(α − β) − cos(α + β) = 2sinαsinβ then, we divide by 2 to isolate the product of sines:. If the. Web the product sum method of factoring we use on trinomials (ax 2 +bx+c) with the value of a=1. Web the area of the large outer square equals the sum of its interior components: Web choose the appropriate pattern and use it to find the product: A2 + 2ab +b2 = (a + b)2 a2 − 2ab +b2 = (a. Because there are factor nodes and variables nodes, we have two types of messages: Web cos(α − β) = cosαcosβ + sinαsinβ − cos(α + β) _ = − (cosαcosβ − sinαsinβ) cos(α − β) − cos(α + β) = 2sinαsinβ then, we divide by 2 to isolate the product of sines:. If the polynomial is of the form x. We just developed special product patterns for binomial squares and for the product of conjugates. Web factoring out common factors. Web the product sum method of factoring we use on trinomials (ax 2 +bx+c) with the value of a=1. Web there is a method that works better and will also identify if the trinomial cannot be factored (is prime). = 6 x 2 + 3 x = 3 x ( 2 x + 1) . If a and b are real numbers. = x 2 + 7 x + 12 = ( x + 3) ( x + 4) . Web this is the pattern for the sum and difference of cubes. Because there are factor nodes and variables nodes, we have two types of messages: Web the area of the large outer square equals the sum of its interior components: ( a + b ) ( a + b) = a ² + 2 ab + b ². Web choose the appropriate pattern and use it to find the product: There are a finite number. Web here is the pattern—the reverse of the binomial squares pattern. Sums and products of roots. Web this is the pattern for the sum and difference of cubes.
Factoring Trinomials using the SumProduct Method YouTube

PPT The SumProduct Algorithm PowerPoint Presentation, free download

Ch3 Expand and Factor with Product Sum pattern YouTube

application of the sum and product rule explained YouTube

How to Factor using the Sum & Product Method YouTube

Factor Trinomials with Leading Coefficient Sum Product Method YouTube

MEDIAN Don Steward mathematics teaching sum and product
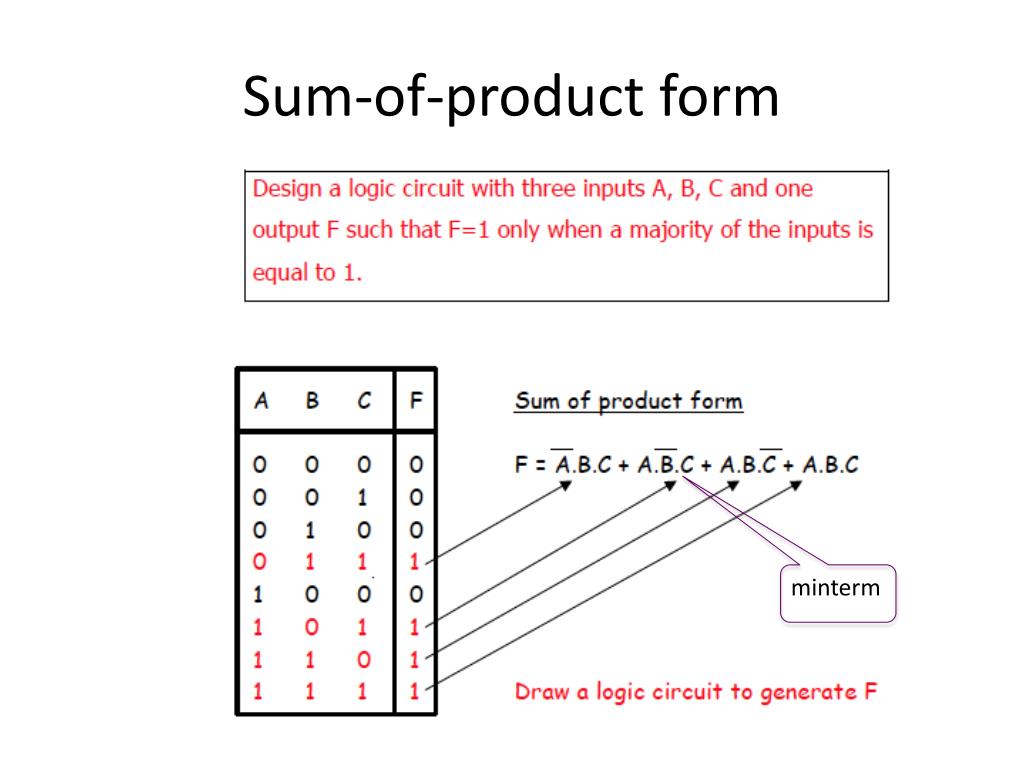
PPT 22C19 Discrete Math Boolean Algebra & Digital Logic PowerPoint

PPT The SumProduct Algorithm PowerPoint Presentation, free download

Product To Sum Identities and Sum To Product Formulas Trigonometry
Web What Is The Sum Product Pattern?
A2 + 2Ab +B2 = (A + B)2 A2 − 2Ab +B2 = (A − B)2 A.
We Will Write These Formulas First And Then Check Them By Multiplication.
68 = 22 ∗ 17 68 = 2 2 ∗ 17 So The Only Options Are 1 1 And 22 ∗ 17 = 68 2 2 ∗ 17 = 68, Or 2 2 And 2.
Related Post: