The First Term In This Number Pattern Is 7
The First Term In This Number Pattern Is 7 - {1, 2, 4, 8, 16, 32,.} is an infinite sequence where every term. So, the logic is adding 5 and subtracting 2. The first term is 7. Recursive formulas give us two pieces of information: The ( n + 1 ) represents the sum of the last term (n) and the first term (1). Web the first term in this number pattern is 7. Web however, the provided answer seems to be incorrect as it does not follow the pattern. We use t1 to represent the 1st term, t2 to represent the 2nd term, t3 to represent the 3rd term and. This question hasn't been solved yet! In this pattern 7 is the first term. 7,12,10,15,13,dots what is the eighth term in this pattern? Type the number in the box. 18 (since 15 + 3 = 18, following the pattern) 8th. Web the first term of the sequence is 5 and the common difference is 3. Web the number pattern is formed by adding 5 to the previous term and then subtracting 2 from the. Web the 1st, 2nd, 3rd, 4th and 5th terms are 2, 7, 12, 17, and 22 respectively. Recursive formulas give us two pieces of information: Web however, the provided answer seems to be incorrect as it does not follow the pattern. Web so the first term in each of these coordinates is pattern a, or in each pair is pattern. The correct calculation should be: Recursive formulas give us two pieces of information: In this section, we will explore the concept of number patterns and focus specifically on a pattern where the first term is. Here the the 1st term is 7. Web however, the provided answer seems to be incorrect as it does not follow the pattern. Web {1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence) {4, 3, 2, 1} is 4 to 1 backwards. \(t_1\) is the first term of a sequence. So pattern a goes from 1, to 2, to 4, to 8, to 16, to 32. This question hasn't been solved yet! So it. In this section, we will explore the concept of number patterns and focus specifically on a pattern where the first term is. \begin {split} t_0 &=0 \\t_ 1&=1 \\t_ 2&=3 \\t_ 3&= 6\\t_ 4&=10 \end {split} t 0t 1t 2t 3t 4 =0=1= 3=6= 10. Web the first term in this number pattern is 7, 7, 12, 10, 15, 13.. \(t_4\) is the fourth term of a. Web the first set of triangular numbers are: Here the the 1st term is 7. Web the first term in this number pattern is 7. Web this arithmetic sequence has the first term [latex]{a_1} = 4[/latex], and a common difference of −5. Web the first term in this number pattern is 7, 7, 12, 10, 15, 13. Ordered lists of numbers like these are called sequences. So it looks like pattern a, to go from the first. Here the the 1st term is 7. Web this arithmetic sequence has the first term [latex]{a_1} = 4[/latex], and a common difference of −5. \begin {split} t_0 &=0 \\t_ 1&=1 \\t_ 2&=3 \\t_ 3&= 6\\t_ 4&=10 \end {split} t 0t 1t 2t 3t 4 =0=1= 3=6= 10. The correct calculation should be: Web so the first term in each of these coordinates is pattern a, or in each pair is pattern a. \(t_1\) is the first term of a sequence. What is the eighth. Alright, now let's look at this last one. View the full answer answer. Type the number in the box. The correct calculation should be: Web here the given sequence is 7, 12, 10, 15, 13,. What is the eighth term in this pattern? Ordered lists of numbers like these are called sequences. \(t_1\) is the first term of a sequence. Here the the 1st term is 7. Each number in a sequence is called a term. Dividing by 2 gives us. We can get any term in the sequence by taking the first term 5 and adding the common difference 3 to it. So, the logic is adding 5 and subtracting 2. In this pattern 7 is the first term. 7,12,10,15,13,dots what is the eighth term in this pattern? In this section, we will explore the concept of number patterns and focus specifically on a pattern where the first term is. Web the first set of triangular numbers are: \(t_4\) is the fourth term of a. We use t1 to represent the 1st term, t2 to represent the 2nd term, t3 to represent the 3rd term and. 18 (since 15 + 3 = 18, following the pattern) 8th. What is the eighth term in this pattern? The correct calculation should be: Web the pattern here, it's not adding a fixed amount, it's multiplying each number by a certain amount, by 2 in this case, to get the next number. The ( n + 1 ) represents the sum of the last term (n) and the first term (1). Web the first term in this number pattern is 7. Here the the 1st term is 7.
number patterns first grade

Number Pattern Block Templates

13 Best Images Of Free Pattern Sequence Worksheets Nu vrogue.co

Understanding number patterns YouTube
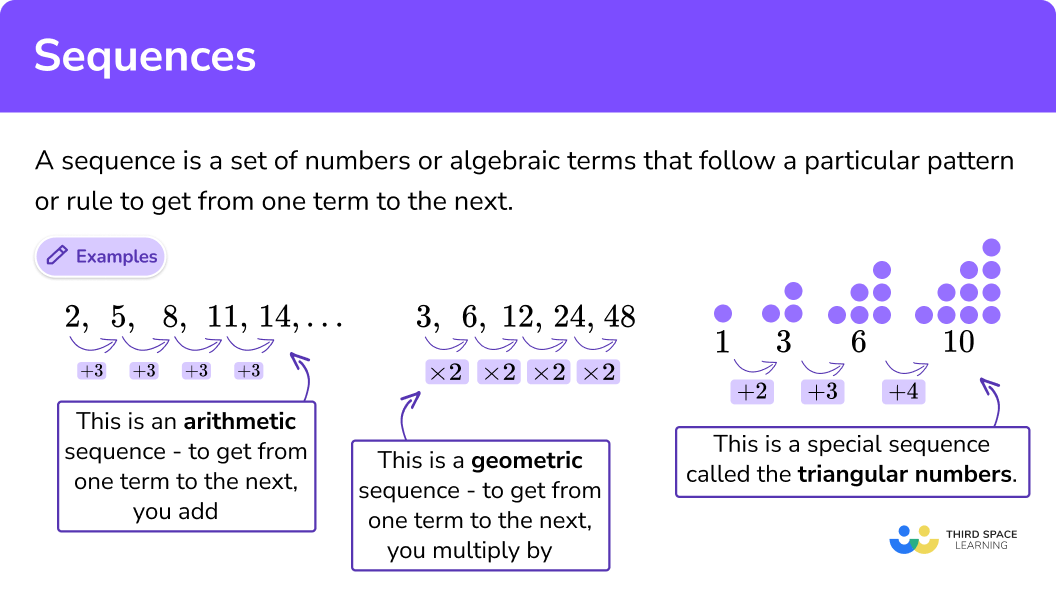
Arithmetic Sequence Patterns
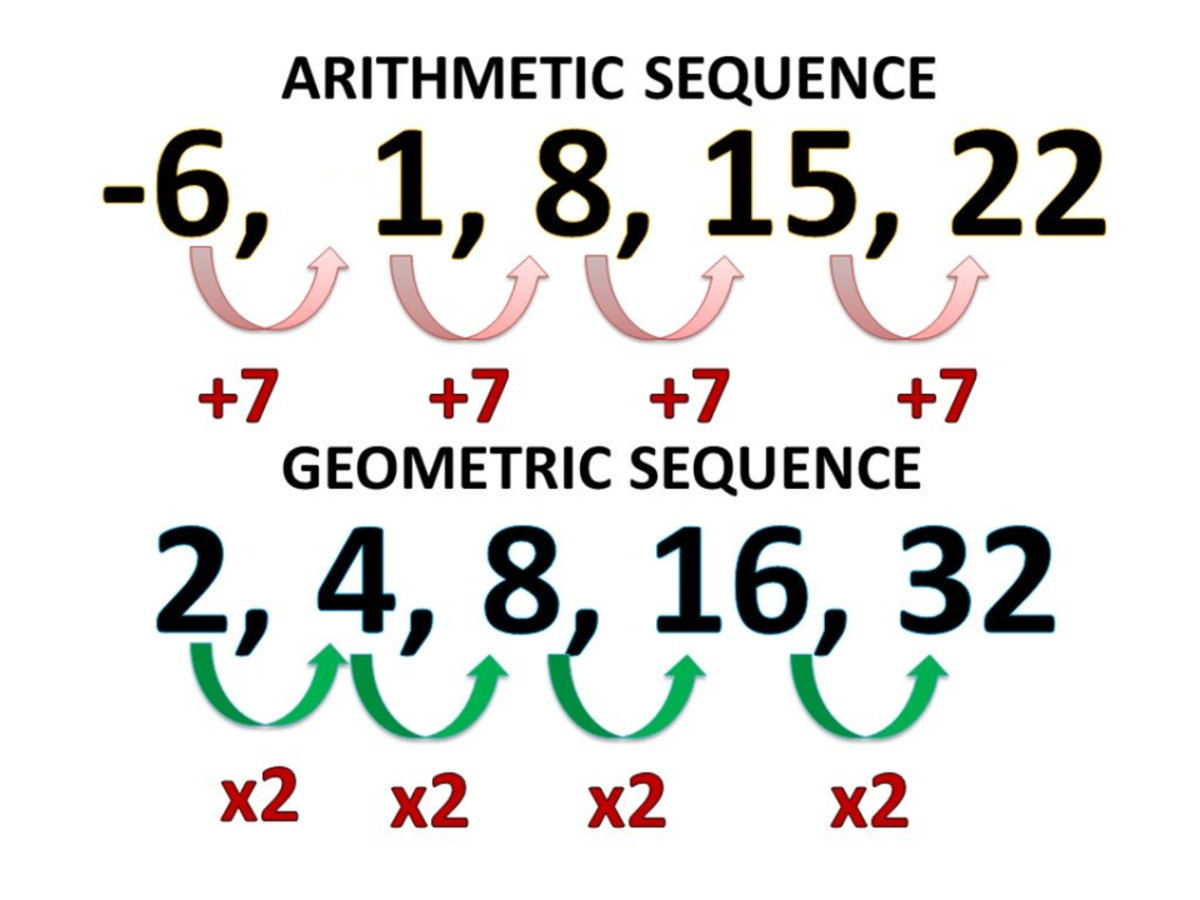
Arithmetic Sequence Patterns

How to Find the General Term of Sequences Owlcation

Quadratic Number Pattern YouTube

MEDIAN Don Steward mathematics teaching extending and generalising

How to Find a Number of Terms in an Arithmetic Sequence Wiki Algebra
Web However, The Provided Answer Seems To Be Incorrect As It Does Not Follow The Pattern.
In This Pattern 7 Is The First Term.
\(T_1\) Is The First Term Of A Sequence.
\Begin {Split} T_0 &=0 \\T_ 1&=1 \\T_ 2&=3 \\T_ 3&= 6\\T_ 4&=10 \End {Split} T 0T 1T 2T 3T 4 =0=1= 3=6= 10.
Related Post: