Quadratic Function Pattern
Quadratic Function Pattern - For exponential functions, the ratio between successive outputs is a constant. 5 × 7 + 1 = 36. 2 × 4 + 1 = 9. A, b and c are known values. Web a quadratic function is any function defined by a polynomial whose greatest exponent is two. You know that for linear functions, the difference between successive outputs is a constant. That means it can be written in the form \ (f (x)=ax^2+bx+c\), with the restrictions that the parameters \ (a\), \ (b\), and \ (c\) are real numbers and \ (a\) cannot be zero. The quadratic formula calculator finds solutions to quadratic equations with real coefficients. The standard form of a quadratic equation looks like this: X is the variable or unknown (we don't know it yet) here are some examples: Web we've seen linear and exponential functions, and now we're ready for quadratic functions. For example, f(x) = x^2 is a quadratic function. In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. An2 + bn + c an2 + bn + c. Web in mathematics, a quadratic equation (from latin quadratus '. A quadratic function has a minimum of one term which is of the second degree. It also can help us to graph these relations/functions. Web in this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Web in mathematics, a quadratic equation (from latin quadratus ' square ') is an equation that can be. It also can help us to graph these relations/functions. You know that for linear functions, the difference between successive outputs is a constant. Web the quadratic sequence formula is: Since the highest degree term in a quadratic function is of the second degree, therefore it is also called the polynomial of degree 2. Web quadratic functions are polynomial functions of. Is there some similar pattern for quadratic functions? Since the highest degree term in a quadratic function is of the second degree, therefore it is also called the polynomial of degree 2. For equations with real solutions, you can use the graphing tool to visualize the solutions. X = −b±√b2 −4ac 2a x = − b ± b 2 −. Working with quadratic functions can be less complex than working with. Is there some similar pattern for quadratic functions? Web a quadratic function is any function defined by a polynomial whose greatest exponent is two. Web the quadratic sequence formula is: Web in mathematics, a quadratic equation (from latin quadratus ' square ') is an equation that can be rearranged. Web gain more insight into the quadratic formula and how it is used in quadratic equations. Web factoring using structure involves recognizing patterns in expressions, like the difference of squares or perfect square trinomials, and using these patterns to break down complex expressions into simpler ones. If the parabola opens up, the vertex represents the lowest point on the graph,. Web in this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Web in mathematics, a quadratic equation (from latin quadratus ' square ') is an equation that can be rearranged in standard form as [1] where x represents an unknown value, and a, b, and c represent known numbers, where a ≠ 0.. Working with quadratic functions can be less complex than working with. The next few problems will help you decide. Web a quadratic function is a polynomial function with one or more variables in which the highest exponent of the variable is two. Web in this lesson, they continue to work with patterns but begin to see these relationships as quadratic. For exponential functions, the ratio between successive outputs is a constant. 5 × 7 + 1 = 36. It also can help us to graph these relations/functions. You know that for linear functions, the difference between successive outputs is a constant. The quadratic formula helps you solve quadratic equations, and is probably one of the top five formulas in math. A quadratic function has a minimum of one term which is of the second degree. The quadratic formula calculator finds solutions to quadratic equations with real coefficients. Web gain more insight into the quadratic formula and how it is used in quadratic equations. In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion.. Web factoring using structure involves recognizing patterns in expressions, like the difference of squares or perfect square trinomials, and using these patterns to break down complex expressions into simpler ones. Web a quadratic function is any function defined by a polynomial whose greatest exponent is two. Click below to see what charlie said: This section will explore patterns in quadratic functions and sequences. Working with quadratic functions can be less complex than working with. We can use the quadratic sequence formula by looking at the general case below: Charlie has been playing with calculations again. Web we've seen linear and exponential functions, and now we're ready for quadratic functions. One important feature of the graph is that it has an extreme point, called the vertex. Play with the quadratic equation explorer so you can see: In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Let’s use this to work out the nth nth term of the quadratic sequence, 4,5,8,13,20,. For example, f(x) = x^2 is a quadratic function. An2 + bn + c an2 + bn + c. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. A, b and c are known values.
Quadratic Expressions Definition Graphs Examples Cuemath

Quadratic Patterns Reflections in the Why
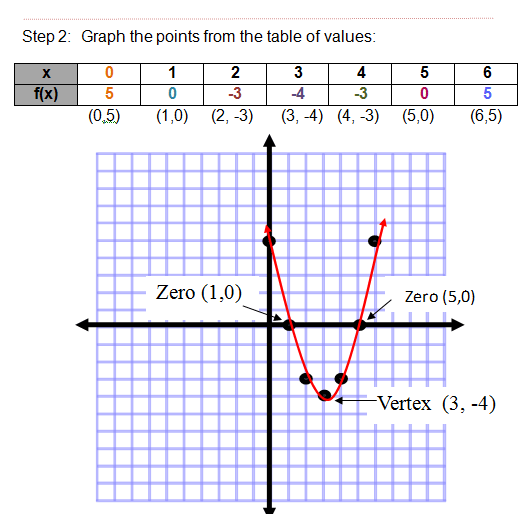
Quadratic Functions
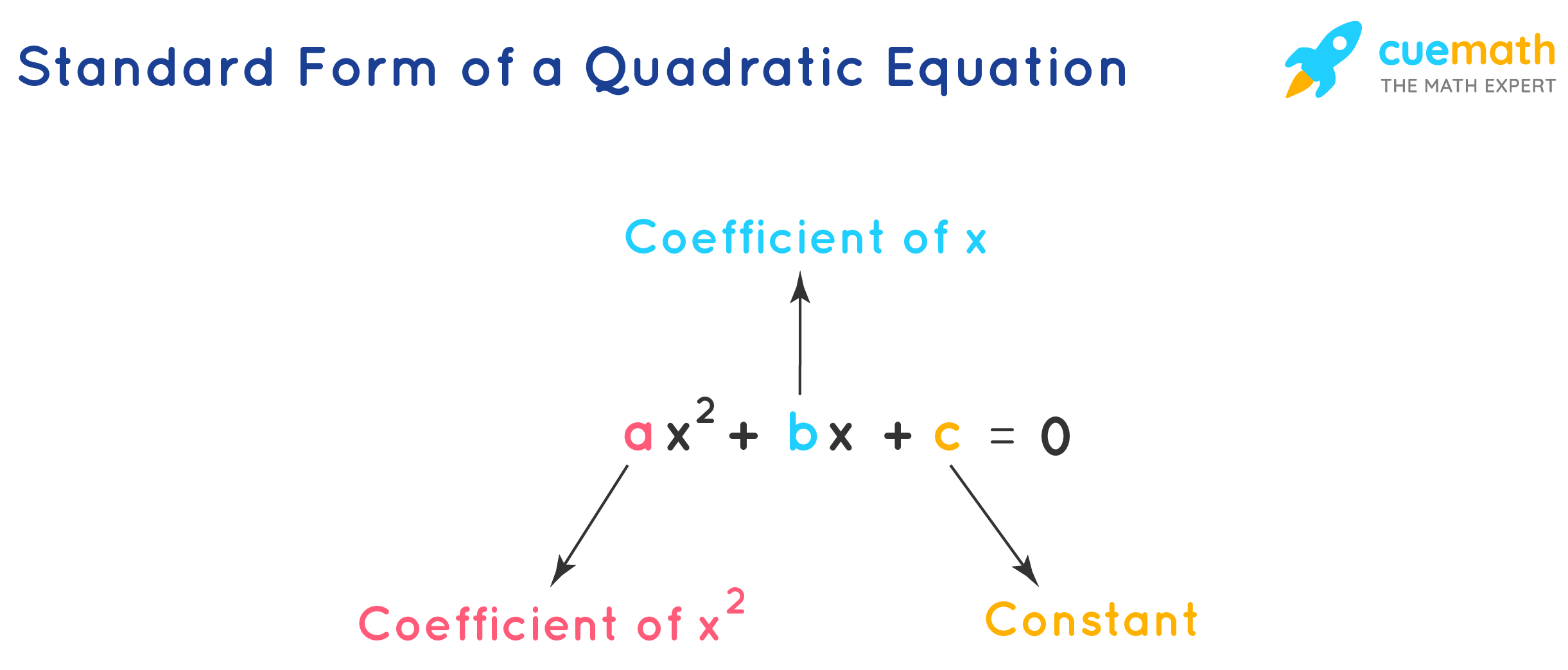
Quadratic Equations Formulas, Methods, and Examples

Quadratic patterns K YouTube
Graphs of Quadratic Functions CK12 Foundation

Writing the equation of a quadratic number pattern YouTube
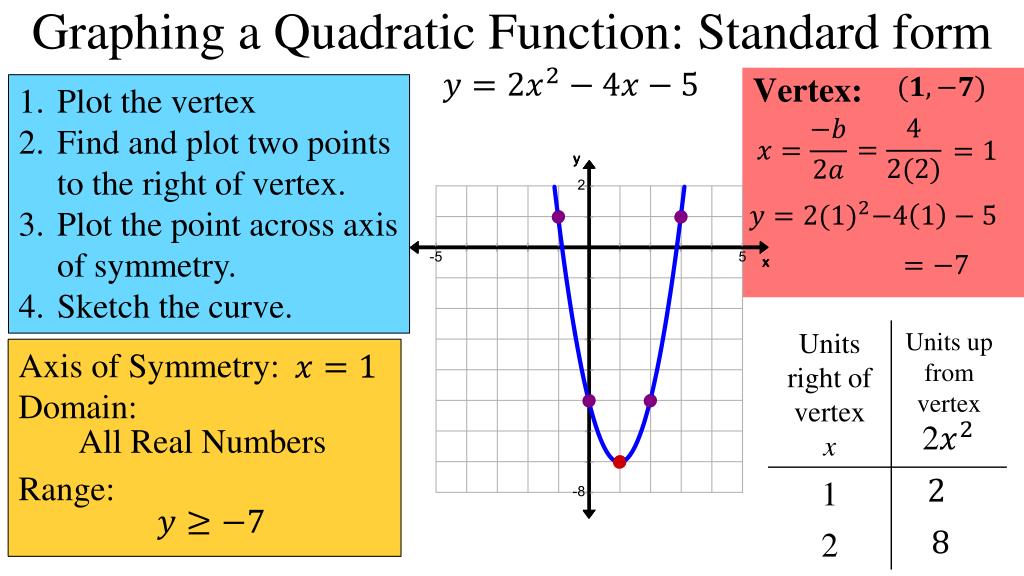
PPT Quadratic Functions Standard Form PowerPoint Presentation, free

Forms of a Quadratic Math Tutoring & Exercises

Quadratic Patterns Video YouTube
Is There Some Similar Pattern For Quadratic Functions?
Since The Highest Degree Term In A Quadratic Function Is Of The Second Degree, Therefore It Is Also Called The Polynomial Of Degree 2.
Where, A,B A,B And C C Are Constants (Numbers On Their Own) N N Is The Term Position.
X Is The Variable Or Unknown (We Don't Know It Yet) Here Are Some Examples:
Related Post:
